共识(Common Knowledge)
@2017.2.6
在看分布式系统的问题时从一篇文章中看到了common knowledge这个词汇,当时心生疑问,共识不就是大家都同意的东西么?这么简单的概念居然在维基百科上会有自己专属的词条?真是好奇害死猫,疑问让我不知深浅的跳到了Wikipedia去一探究竟。谁知不看不知道,一看懵逼了。一个“简单”的共识概念可以扯出上下五千年来。这篇笔记算是对维基百科词条的一个整理和消化,可能还存在诸多讹误。
何谓共识
共识是(或者几乎)所有人都知道的知识(信息) ,常常作为术语被在社区中使用。共识无需考虑特定的主题,比如科学或者历史,相反共识可以关于更加广泛的主题,例如科学、文学、历史和娱乐等等。共识通常无需引用,共识与“常识”不同,“常识”已经被不同的心理学家定义成“一定范围内的非专家媒介交流的具备文化价值的知识”了,并且被认为是与智力相关的某个因素。因此,常识与共识有着显著的不同。
广义上,共识用于指代那些可以被读者作为有效信息接受的信息,例如很多人可能都知道的信息。作为一个示例,这类信息可以包括水的冰点和沸点。如何判断信息是否为共识?你可以问问自己你的听众是谁。你是否可以假设他们已经对主题有一定的熟悉度了,或者信息的可信度是否有问题。
有些称为“共识”的东西有时候与argumentumad populum (拉丁语:揭露给人们看)谬论有关。argumentumad populum谬论警告人们这种假设:仅仅只是因为每个人都相信某些事情是真的,那么它就一定是真的。错误的信息经过传递很容易变成谣言。
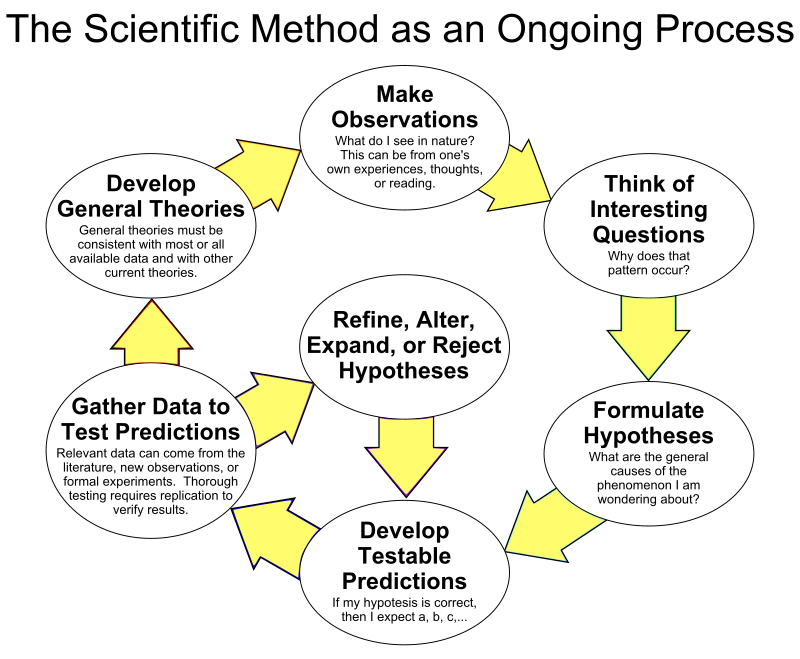
已经有很多技术发展出来用以应对区分真相和已经成为所谓的”共识的事实”这样的问题。科学的方法通常用于与天文学、数学、物理学以及自然的基本规律相关的现象研究。科学的方法通常是一个循环往复的迭代过程,通过持续的迭代不断逼近自然的真相。在法律环境下,证据原则通常会排除传闻(可能是利用了某些人相信的”事实“就是”共识“)。
共识示例
- ”巴黎是法国的首都“。很多国家的首都城市对大部分人来说都是共识。
- ”月亮绕着地球旋转“。对月亮的观察让显示它是这样运转的。进一步的说,科学发现给出了确认)。在历史上的很多时期,人们认为地球是平的,太阳绕着地球在旋转是一个共识,但是后来都被证实是错误的。
- ”把氨水和漂白粉混合是危险的“。即使两者都是常见的日化用品,但是将两者混合导致的事故也是很罕见的。这是因为两者混合后产生的致命化学反应是一个流传很广的说法。
- "美国宪法第五修正案赋予美国公民在法庭上可以拒绝回答那些可能使自己有罪的问题"。”申请第五修正案“在美国口语中是一个常见的短语,即使在流行的“查普尔秀”这样流行的电视系列剧中也是如此。因此,这在美国可以认为是一个共识。
共识逻辑
共识是对一组代理来说一种特殊的知识。我们说在一组代理中有一个共识,当且仅当中所有的代理都知道,他们(所有代理)都知道他们(所有代理)知道,他们(所有代理)都知道他们(所有代理)知道,如此递归直到无穷无尽的天涯海角。
这个概念由David Kellogg Lewis 在其哲学著作Convetion(1969)中首次引入。社会学家Morris Friedell在1969年的论文#cite_note-2)中定义了共识。1976年Robert Aumann在集合论框架上首次对共识赋予了数学形式。从1980年代开始,计算机科学家对知识逻辑,特别对共识的兴趣与日俱增。有大量的基于共识概念的问题被数学家们进行了扩展研究,比如John Conway。
哲学家 Stephen Schiffer在它的书《Meaning》中独立发展了他称之为“互识”的概念,其功能与Lewis的共识非常相似。
示例
猜想
共识的问题常常通过下面这个猜想的变体来引入:
在一个小岛上,有个蓝色眼睛的人,其余都是绿色眼睛的人。猜想开始时,岛上的居民没有人知道他们自己眼睛的颜色。按照规则,如果岛上某个人发现自己的眼睛是蓝色的,那么这个人必须在黎明之前离开小岛。没有发现这个秘密的人通常都是一觉睡到天亮。在这个小岛上,每个人都知道其他人眼睛的颜色,没有可以反射的光滑面,也没有关于眼睛颜色的讨论。
某天,一个外人来到岛上,把岛上所有人都召集到一起,然后作出如下公开宣言:“你们中间至少有一个人的眼睛是蓝色的”。进一步地讲,这个陌生人被认为是诚实的,并且岛上的所有人都知道他是诚实的,如此递归下去:这个陌生人是诚实的就是一个共识,因此岛上的居民中至少有一人的眼睛是蓝色的也就成了一个共识。问题是:假设岛上的居民都是完全具备逻辑性的,并且这也是一个共识,那么最终会怎样?
答案
答案是,在宣布声明之后的第个黎明,所有蓝色眼睛的人都会离开这个小岛。
证明
这个答案可以通过归纳法证明。
如果,也就是说小岛上有且只有一个蓝色眼睛的居民。这个人将会发现自己是蓝色的眼睛(通过观察其他人都是绿色的眼睛),然后在第一个()黎明之前离开小岛。
如果,在第一个黎明之前不会有人离开。那两个蓝色眼睛的人第一天发现只有一个人是蓝色的眼睛,因此在第一个黎明之前没有人离开小岛(因此,),但是会在第二个黎明之前全部离开(假设这两个蓝色眼睛的人是A和B,第一天A看到B是蓝色眼睛,B也看到A是蓝色眼睛,他们都以为对方会知道自己就是那个应该离开的人,但是并不知道自己也是蓝色的眼睛。但是第二天,他们发现对方都没离开,此刻他们会意识到自己也是那个蓝色眼睛的人,于是在第二天会离开)。以此类推,在第一个黎明之前不会有人离开小岛,当前仅当小岛上至少有个蓝色眼睛的居民。那些蓝色眼睛的人会看到 个蓝色眼睛的人混杂在人群中,并且知道肯定至少有个蓝色眼睛的人,从而推断他们自己也一定是蓝色的眼睛,从而选择离开小岛。
这个场景最有趣的地方是,对于大于 1,外来者只是告诉岛上的居民们本已知道的事实:在他们中间有蓝色眼睛的人存在。然后,在这个事实被宣布之前,这个事实本身并不是一个共识。
对于,这只是“一级”知识,每个蓝色眼睛的人都知道有另外一个人是蓝色的眼睛,但是每个蓝色眼睛的人之并不知道另一个蓝色眼睛的人也知道这个事实。
对于,这是“二级”知识,2天以后,每个蓝色眼睛的人都知道有第二个具有蓝色眼睛的人知道存在第三个具有蓝色眼睛的人,但是没人知道第三个具有蓝色眼睛的人知道这个事实,直到第三天来临。
一般的,对于大于1,是“级”知识。天以后,每个蓝色眼睛的人都知道第二个具有蓝色眼睛的人知道有第三个具有蓝色眼睛的人知道。。。(重复到级)有第个人有蓝色的眼睛。但是没人知道有一个第“个”人知道这个事实,直到第天来临。共识的概念因此有一个可推出的效应。知道每个人知道确实可以有所作为。当这个外来者的公开声明(每个人都已经知道的事实)成为一个共识,小岛上具有蓝色眼睛的居民最终都会推断其自身的状态并离开小岛。