两将军与拜占庭将军问题
@2017.1.19
在研究Paxos协议时看到了与分布式一致性问题有关的两个经典问题:两将军问题和拜占庭将军问题。为了把问题弄清楚,特地把维基百科上的关于这两个问题的词条从头到尾过了一遍,这篇笔记和上一篇共识类似,基本上是维基百科词条的翻译,作为理解问题过程的记录。
在计算机学科中,两将军问题是一个思想实验,用于揭示在一个不可靠的链接上通过通信来协调统一的行动所面临的设计挑战和缺陷。“两将军问题”与更加通用的拜占庭将军问题有关(虽然它比后者发表的时间要早得多),尽管“两将军问题”适用于所有两方参与者可能出现失败的通信系统中,但是通常在关于计算机网络的入门课程中出现(特别是在传输控制协议中说明TCP为什么无法保证不同节点之间状态的一致性及其原因)。在认识逻辑中,一个重要的原则是问题强调了共识的重要性。有些作者也将其称为两将军悖论、两军问题或者协同攻击问题。两将军问题是第一个被证实的计算机通信无解问题,该证明的一个重要结论是类似于拜占庭将军问题的问题在面临无法预知的通信错误时都是无法解决的,从而为分布式一致性协议提供了切实可行的预测基础。
定义
有两支军队分别由不同的将军率领,准备攻打一座带有防御工事的城市。军队驻扎在城市附近的两个不同的山谷中,这两座山被第三个山谷从中间一分为二。两位将军之间唯一的通信方式是派遣信使穿过中间的山谷。但不幸的是,中间的山谷被城市的守军占领了,并且所有穿过该山谷信使都可能被抓获。
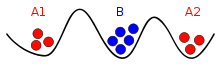
军队位置
A1军与A2军需要互相通信,但是他们的信使可能会被B军抓获。
两位将军在对进攻达成一致时,尚未对进攻时间统一意见。为了稳操胜券,需要两个将军指挥他们的军队同时对这座城市发起进攻,否则单独进攻的军队就是自取灭亡。因此两位将军必须互相通信以决定进攻时间,并且同意在那个时间进攻。 每位将军都必须知道另一位将军知道两人对作战计划已经达成一致。由于消息接收方的应答)和原始消息一样可能很容易就丢失,这里隐藏了这样一个事实:需要无限的消息序列来达成一致)。
这个思想实验包括他们如何才能达成一致的过程。"两将军问题"最简单的形式中,有一位将军是Leader身份,他来决定进攻的时间,并且必须将这个时间传达给另一位将军。这个问题引出将军可以使用的算法,包括:发送消息和处理回执消息,从而使他们可以正确的得到如下结论:
是的,我们两支军队将在协商好的时间同时发起进攻。
允许这样的话,那么将军们对进攻时间达成一致就非常简单了(比如,一条带有成功的回执的消息)。"两将军问题"的精妙之处就在于无法为将军们设计出可以安全使用的可以达成上述协议的算法。
问题演示
第一个将军可能发送一条消息"在8月4日早晨 9点发起进攻"。但是,消息一旦发出,第一个将军就无法知道信使是否通过了敌军山谷。这种不确定性可能导致第一个将军由于担心自己成为单一攻击者的风险而对进攻犹豫不决。
如果确认消息送达,第二个将军可能向第一个将军发送一条确认消息:"我收到了你的消息,并且将在8月4日早晨9点发起进攻"。但是,携带确认消息的信使可能会被敌军抓获,这样第二个将军也会犹豫,因为他知道第一个将军可能因为没有收到确认信息而中止进攻。
进一步的确认消息看上去像是一个解决方案,让第一个将军向第二个将军发送一个二次确认消息:"我已经收到你对在8月4日早晨9点发起进攻的确认回执了"。但是,第一位将军派遣的新信使也可能被敌军抓获。因此,我们很快就可以得出结论,无论发起多少轮的消息确认,也无法保证第二个必要条件成立:每个将军都确认对方已经同意了进攻计划。
两个将军总是处于等待其最后一条消息是否通过敌军山谷的焦虑中。
证明
具有固定消息数量的确定性协议
因为协议是确定性的,假设有一个固定数量的消息序列,其中有一条或者多条消息成功送达,也有一条或者多条消息未能成功送达。假设是,两位将军之间必须有一个共享的两军都会发起进攻的决议。
考虑最后一条成功投递的消息。如果最后一条消息未能成功投递,那么至少有一位将军(很可能是接收者)将会决定不发起进攻。从最后一条消息的发送方视角来看,不管怎样,发送和投递消息的顺序与其该有的顺序完全相同,说明那条消息已经投递出去了。
由于协议是确定性的,发送最后一条消息的将军仍然会发起进攻。我们现在已经创建了一种情况,推荐的协议导致一个将军发起进攻而另一个将军却中止进攻,这就与假定该协议可以解决这个问题自相矛盾了。
非确定性变长协议
一个带有变化的消息数量的非确定性协议可以比拟成一个"有限树",树中的每个叶子或者分支(节点)代表截止某个点为止已经发现的示例。
树的根用初始消息标识,从这些根节点衍生的分支节点用初始消息的下一条消息标识。叶子节点代表发送最后一条消息之后的示例。在发送任何消息之前就终止的消息用一棵无效的(null)树表示。
假设存在一个可以解决问题的非确定协议,那么与前面章节描述的确定性示例的争论相似,通过移除树中所有叶子节点后得到确定性的示例,那么该确定性示例可以解决这个问题。
由于非确定协议是有限的,一棵空(Empty)树表示的协议可以解决问题,很明显这是不可能的。因此也不存在可以解决"两将军问题"的非确定性协议。
工程实践
处理”两将军问题“的可编程方式应该使用这样的模式:接受通信信道的不确定性,不试图消除这种不确定性。同时,应该将不确定性降到到可接受的程度。比如,第一个将军可以派出100个信使,期望这100人全部被抓的概率很低。基于这种方式第一个将军无论如何都将发起进攻,而第二个将军只要收到消息也会发起进攻。替代方案是第一个将军可以发送一个消息流,第二个将军可以对其收到的消息流逐个发送确认消息。每收到一条消息将军们的信心都会增加。正如证明中看到的,没人可以确认进攻肯定可以被协调好。不存在他们可以使用的算法(例如,如果收到4条以上的消息就发起进攻)保证不出现只有一方发起进攻的情况。当然,第一位将军可以在每条消息上增加一个标识,表示这条消息的次序1,2,3…..n。这个方法可以让第二个将军知道信道的可靠性,然后回复一定数量的消息,确保接收者有很高的概率可以接收到至少一条消息。如果信道被认为是足够可靠的,那么一条消息就足够了,多余的消息也于事无补。最后一条消息很可能像第一条消息一样丢失。
假设每当派出的信使被截获时,将军们都必须派遣一名新的信使。可以设计一个算法用最少的信使就可以保证获得协调进攻所需的足够高的信心。为了减少完成协调进攻时牺牲的信使人数,将军们可以同意将信使的消失作为发起消息的将军至少已经接收到了一条回执的标志,并且保证会发动进攻。假设一个信使通过危险区域需要花费1分钟,在收到回执后允许200分钟的静默期,可以使我们无需派遣更多的信使就能得到很高的信心。这种情况下,信使仅在一方未接收到进攻时间时使用。当200分钟静默期结束时,每个将军都可以推断:我已经有200分钟没有接收到新消息了,要么是这期间的200个信使都没能闯过危险区,要么意味着对方已经确认并保证会发起进攻,那么我需要这样做。”
历史
两将军问题及其无解的证明首次出现在由E.A.Akkoyunlu,K.Ekannadham,和R.V.Huber于1975年发表的论文“网络通信设计中的一些限制与妥协”^2^中,在关于两组匪徒通信的上下文环境中从第73页开始描述。
这个问题被JimGray在1978年发表的“数据库操作系统比较”^3^第465页中命名为“两将军悖论”。这也是被广泛引用的关于这个问题的定义和误解证明的来源,虽然发表时间并不是最早的。
拜占庭将军问题
因为Leslie Lamport在论文中提出了拜占庭将军问题,从而使这个问题流传甚广。那么什么是拜占庭将军问题呢?其实是Leslie Lamport偷用了所谓的“中国将军问题”,也就是本文所述的“两将军问题“中的想法,并加入了新的假设条件,提出的新问题,他加入的新条件是:
- 将军的数量不止两个,而是很多个将军
- 这些将军中存在叛徒
作者在提出这个新的问题时为了避免冒犯读者,选择了当时完全封闭的社会”阿尔巴尼亚“作为将军们的祖国,因此称其为”阿尔巴尼亚将军问题“。但是另一个人Jack Goldberg意识到这个世界上在阿尔巴尼亚之外肯定还存在阿尔巴尼亚人,并且阿尔巴尼亚不会永远是一个“黑洞”一样的存在,他建议Leslie Lamport用一个新名字来代替,于是就出现了“拜占庭将军问题”。4
问题
存在这么一组将军,每个人领导一部分拜占庭军队来包围一座城市。这些将军希望制定一份计划来攻击那座城市。在最简单的形式中,将军们只须决定是进攻还是撤退。有些将军可能倾向于进攻,而其他人可能想撤退。最重要的是,每个将军都同意一个共同的决议:少部分将军发起的非全力进攻可能会溃败,这比一次协调一致的进攻或者撤退都要更糟糕。
将军中存在叛徒时这个问题就复杂了。这些叛徒将军不仅可能投票给一个不好的方案,他们还可能有选择的去做这件事。比如,如果有9位将军投票,其中4人支持进攻而且另外4人支持撤退,那么第9位将军可以投票给那些支持撤退的将军,同时也投票给那些支持进攻的将军。那些收到9个将军撤退选票的将军会撤退,而剩余的人会开始进攻(对进攻者来说可能并不好)。如果将军们是被分隔开的,必须通过信使发送选票问题就会更复杂,因为选票可能无法成功送达或者被假冒选票替代。
如果忠诚的(不是靠不住的)将军对他们之间的策略有个一致的决议,那么拜占庭容错是可以达成的。需要注意的是,对于丢失的消息可以有一个默认的选票值。比如,丢失的消息可以赋值为Null。进一步讲,如果Null选票占多数,可以使用一个预先分配的默认策略(例如,撤退)。
这个问题在计算机系统中的典型映射是计算机就是那些将军,他们之间的数字通信系统链路就像信使。
已知的拜占庭错误示例
在两份等价的论文中给出了很多拜占庭错误的例子34。这些例子在NASA的DASHlink网页中有描述,这些网页中也描述了一些可能导致拜占庭错误的现象。
拜占庭错误在新建的佛吉尼亚级核潜艇的耐力测试中很罕见也不寻常,至少在2005年是这样的(问题公开报道的时间)。
早期方案
Lamport,Shostak和Pease在1982年的论文中描述了一些方案。他们认为将军问题可以简化为解决一个“司令和中尉”问题,这里忠诚的中尉们必须步调一致,并且只要司令是忠诚的,那么他们的动作必须服从司令的命令。
- 一个方案考虑的是消息可能会被篡改的情况,只要叛徒将军的数量小于将军数量的1/3拜占庭容错就可以达成。无法处理大于等于1/3的叛徒可以降维成证明如果司令是叛徒,那么”一个司令和两个中尉“问题是无解的。为了证明这点,假设我们有一个叛徒司令A,与两个中尉B和C。当A告诉B攻击,C撤退,并且让B和C互相给对方发送消息传达A的命令,这时不论是B还是C都无法指出谁是叛徒,因为不可能是A---另一个中尉可能篡改了来自A的消息。可以表明,如果将军总数是,其中叛徒的数量是,那么当且仅当时该问题有解,并且通信是同步的(带有延迟)5
- 第二个方案需要无法篡改的消息签名。对于安全敏感的关键系统,数字签名(在线代计算机系统中,可以通过使用公钥加密实现)在存在任意数量的叛徒将军的情况下可以提供”拜占庭容错“方案。虽然如此,对于安全敏感的关键系统,简单的错误检查代码,例如CRCs以很低的成本提供了相同的或者更好的覆盖。这对拜占庭和非拜占庭错误都有效。因此,加密的数字签名方法对于安全敏感的关键系统并不是一个好的选择,除非存在一个特殊的安全性威胁。但是错误检测代码,例如CRCs是比密码更好的技术,无法为安全性敏感的关键系统提供足够的覆盖率。这是由Schrödinger CRC场景提供的,这个场景中消息带有CRC保护,一个拜占庭错误比特位向不同的观察者展示不同的数据,但是不同的观察者看到的都是以个有效的CRC。
- 并非所有的将军都可以直接互相通信的情况下也存在前两个方案允许的拜占庭容错行为
1980年代设计了很多实现了拜占庭容错的系统,包括Draper的FTMP, 霍尼韦尔的MMFCS和SRI的SIFT。
实际的拜占庭容错方案
1999年,Miguel Castro和Barbara Liskov介绍了”实际的拜占庭如弄错(PBFT)“算法,提供了高性能的拜占庭状态机复制, 每秒钟可以以亚毫秒递增的延迟来处理数千个请求。
PBFT发表之后,很多BFT协议被发展出来提高其健壮性和性能。例如,Q/U, HQ,Zyzzyva,和AbsTRACTs等等,解决了性能和开销问题,其他协议,比如Aardvark和RBFT解决了健壮性问题。不止如此,Adapt试图利用已有的BFT协议,通过根据依赖条件的变化,在协议之间切换来提高系统的的健壮性和性能。而且,BFT协议被用于协调受信的模块缩减其副本数量,例如A2M-PBFT-EA和MinBFT。
软件
UpRight是一个吸纳了很多协议创新的开源库,用于构建崩溃(“up”)和拜占庭行为(“right”)容忍的服务。
除了PBFT和UpRight,还有BFT-SMaRt库,一个用Java开发的高性能的拜占庭容错的状态机复制库。这个库实现了一个和PBFT非常相似的协议,以及一个配套的提供状态转换和主机在线重配置的协议。BFT-SMaRt是最近的实现状态机复制的尝试,仍然处于活跃的维护状态。
Archistar利用一个瘦BFT层用于通信,它在LGPLv2许可证下用Java构建了一个安全的多云存储系统原型,专注于简单性和可读性。它的目标是称为下一步研究的基础。
Askemos是一个并发的、垃圾回收的基于拜占庭容错的状态机复制基础上的持久化编程平台。它构建了智能合约的执行环境原型。
Tendermint是一个用于BFT状态机复制的通用软件。使用socket协议使状态机可以用任何编程语言实现,同时为状态机提供了影响一致性的元素的方式,比如活跃的进程列表。Tendermint以区块链)的形式实现,可以分批承担BFT的开销,而且从错误中恢复的速度更快。
实践
比特币是使用BFT的一个例子,比特币是一个点对点的数字货币系统。比特币网络以并行的方式工作,产生一个散列货币形态的工作量证明链。工作量证明链是用于解决拜占庭错误,使系统状态达到全局一致的关键。
有些航空系统,比如波音777飞机信息管理系统(通过他的ARINC 659 SAFEbus ® 网络)、波音777飞行控制系统以及波音787飞行控制系统都使用拜占庭容错机制。因为这些都是实时系统,他们的拜占庭容错方案必须具备非常低的延迟。例如,SAFEbus对命令可以以一微妙的延迟达到拜占庭容错。
有些飞船,例如SpaceX Dragon飞行系统用他们自己的方式考虑拜占庭容错机制。
拜占庭容错机制使用将收到的消息(或者只是一个签名)向该消息的其他接收者重复的模块。所有这些机制创造了这样一假设,那就是重复一个消息的动作阻塞了拜占庭症状的传播。对于那些有较高安全度或者安全性敏感的系统,这个假设必须证明在一个可接受的错误恢复级别上是成立的。当通过测试提供证明时,其中一个困难是创建一个足够宽的具有拜占庭症状的信号范围。这样的测试通常需要特殊的错误介入。
附录
- Wikipedia Tow generals)
- "Some constraints and trade-offs in the design of network communications"
- "Notes on Data Base Operating Systems"
- https://www.microsoft.com/en-us/research/publication/byzantine-generals-problem/?from=http%3A%2F%2Fresearch.microsoft.com%2Fen-us%2Fum%2Fpeople%2Flamport%2Fpubs%2Fbyz.pdf
- https://en.wikipedia.org/wiki/Byzantine_fault_tolerance#cite_note-9